I’ve been tweaking my pairs trading scripts this week, mainly looking at how renewable energy stocks move together.

A lot of beginners get stuck thinking that if two stocks look correlated, they’ll keep moving in sync.

That's not how it works.

By reading today’s newsletter, you’ll get Python code to detect cointegrated pairs in alternative energy stocks and backtest a simple pairs trading strategy with clear entry and exit rules.

Let's go!

A simple stat arb strategy you can trade now

Pairs trading uses statistical relationships between two stocks to identify mean-reversion opportunities.

They typically taking a long position in one and a short in another.

Cointegration goes deeper than correlation, focusing on pairs where the spread between stocks remains stable over time.

This strategy didn’t come out of nowhere, it’s rooted in market-neutral trading’s evolution.

Pairs trading traces back to the 1980s at Morgan Stanley when computer-driven statistical arbitrage began outperforming traditional trading approaches. Early strategies relied on simple correlations but soon embraced cointegration, popularized by Engle and Granger’s cointegration tests in econometrics. Over the past two decades, professionals have zeroed in on mean reversion, refining pair selection with rigorous statistical methods.

Today, this quantitative approach is standard in hedge funds and prop shops handling liquid, theme-linked equities.

Let’s see how it works with Python.

Imports and setup

We use matplotlib and seaborn for charting, numpy for math, pandas for working with data tables, yfinance for downloading stock prices, and statsmodels for testing relationships between price series.

1import matplotlib.pyplot as plt
2import numpy as np
3import pandas as pd
4import seaborn as sns
5import yfinance as yf
6from statsmodels.tsa.stattools import coint

This block downloads daily closing prices for a group of clean energy stocks and ETFs from yfinance.

1tickers = [
2    "NEE",
3    "FSLR",
4    "ENPH",
5    "PLUG",
6    "BEP",
7    "AQN",
8    "PBW",
9    "FAN",
10    "ICLN",
11]
12start_date = "2014-01-01"
13end_date = "2015-01-01"
14df = yf.download(
15    tickers, 
16    start=start_date, 
17    end=end_date, 
18    auto_adjust=False
19).Close
20df = df.dropna()

We’re collecting a full year of prices for nine tickers focused on renewable energy topics, then making sure there’s no missing data for any of them. This gives us a clean set of price histories lined up by date—one column per ticker—ready for analysis.

Test for cointegration between stock pairs

This block tests for cointegration—whether two price series have a statistically meaningful long-term relationship—between each possible pair of tickers in our set.

1n = len(tickers)
2score_matrix = np.zeros((n, n))
3pvalue_matrix = np.ones((n, n))
4pairs = []
5for i in range(n):
6    for j in range(i + 1, n):
7        score, pval, _ = coint(df.iloc[:, i], df.iloc[:, j])
8        score_matrix[i, j] = score
9        pvalue_matrix[i, j] = pval
10        if pval < 0.10:
11            pairs.append((tickers[i], tickers[j]))

We use the cointegration test from statsmodels for every unique pair of tickers. For each pair, we save both the test’s score and its p-value, recording the result in two matrices. Whenever the relationship looks strong enough to be statistically significant (p-value below 0.10), we print the ticker names and p-value, and add the pair to a list. This helps us spot which stock pairs act in sync over time.

This block finds the pair with the strongest relationship (the lowest p-value), then calculates the difference between their price series and standardizes it using a rolling z-score for the past 21 days.

1mask = np.triu(np.ones_like(pvalue_matrix, dtype=bool), k=1)
2upper_vals = pvalue_matrix[mask]
3min_idx_flat = np.argmin(upper_vals)
4min_p = upper_vals[min_idx_flat]
5idx_pairs = np.column_stack(np.where(mask))
6i, j = idx_pairs[min_idx_flat]
7
8S1, S2 = df.iloc[:, i], df.iloc[:, j]
9
10score, pvalue, _ = coint(S1, S2)
11print(f"tickers with lowest p-value: {tickers[i]} x {tickers[j]}, p={pvalue}")
12spread = S1 - S2
13zscore = (spread - spread.rolling(21, min_periods=21).mean()) / spread.rolling(21, min_periods=21).std()

We examine the matrix of p-values and pull out the pair with the lowest value, signaling the tightest statistical connection over our sample. We then create a daily time series showing the price gap between those two stocks, and calculate how “extreme” it is with a rolling z-score. Standardizing the gap helps us identify when the difference is unusually high or low, which can be a setup for certain trading strategies.

Visualize cointegration results

This block creates a heatmap so we can clearly see which pairs of tickers have close statistical relationships, and which do not.

1mask = np.tril(np.ones_like(pvalue_matrix, dtype=bool)) | (pvalue_matrix >= 0.10)
2plt.figure(figsize=(8, 6))
3sns.heatmap(
4    pvalue_matrix,
5    mask=mask,
6    xticklabels=tickers,
7    yticklabels=tickers,
8    cmap="RdYlGn_r",
9    annot=True,
10    fmt=".2f",
11    cbar=True,
12    vmin=0,
13    vmax=1,
14)
15plt.title("Cointegration Test p-value Matrix")
16plt.show()

The results look something like this.

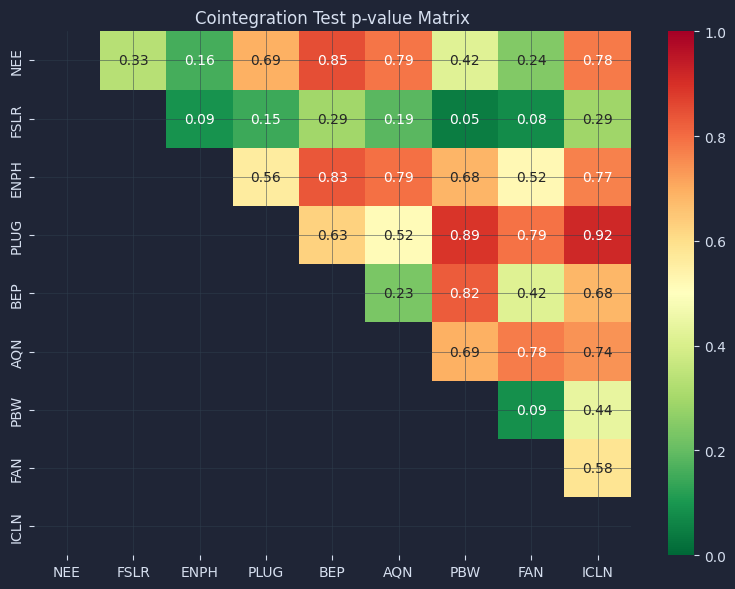
We use seaborn to chart the p-values for all pairs, hiding entries that aren’t meaningful (like the lower half and those above 0.95). Each square shows the exact value, so it’s easy to spot which tickers move alike. The color scale helps us focus on the most promising relationships for strategies or further study.

This block displays the spread and z-score for the pair of tickers with the tightest relationship, highlighting typical and outlying values.

1fig, axes = plt.subplots(2, 1, figsize=(14, 8), sharex=True)
2axes[0].plot(spread.index, spread, label="Spread")
3axes[0].axhline(spread.mean(), color="black", linestyle="--", lw=1)
4axes[0].axhline(spread.mean() + spread.std(), color="red", linestyle="--", lw=1)
5axes[0].axhline(spread.mean() - spread.std(), color="green", linestyle="--", lw=1)
6axes[0].set_ylabel("Spread")
7axes[0].legend()
8axes[1].plot(zscore.index, zscore, label="Z-score")
9axes[1].axhline(0, color="black", linestyle="--", lw=1)
10axes[1].axhline(1, color="red", linestyle="--", lw=1)
11axes[1].axhline(-1, color="green", linestyle="--", lw=1)
12axes[1].set_ylabel("Z-score")
13axes[1].legend()
14plt.xlabel("Date")
15plt.suptitle("Spread and Rolling Z-score between ABGB and FSLR")
16plt.tight_layout()
17plt.show()

The result is a chart that looks something like this.

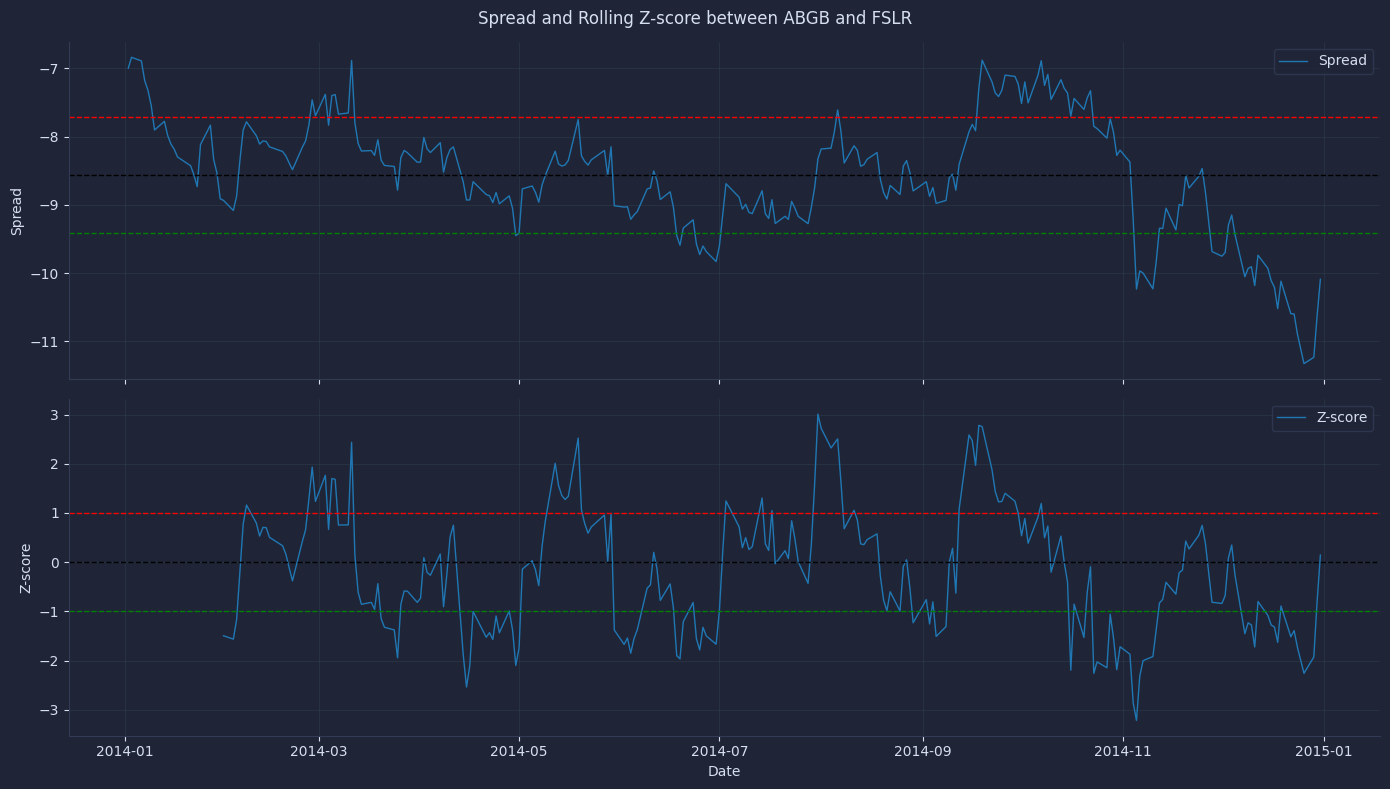
The spread oscillates around its rolling mean and frequently crosses the ±1 Z-score thresholds, indicating repeated mean-reversion opportunities. A trader would buy ABGB and short FSLR when the Z-score falls below −1, expecting the spread to rise back toward zero, and reverse the position (short ABGB, long FSLR) when the Z-score exceeds +1.

Position sizing should balance dollar exposure or hedge ratio weights so the trade isolates relative value rather than market beta, then exit as the Z-score converges back toward zero to lock in the mean-reversion profit.

Your next steps

You can now spot statistically linked stock pairs and see their price gaps in action. Try swapping in different tickers or extending the date range to see if relationships hold over time. Adjust the rolling window length to test how sensitive your z-scores are to recent moves. This hands-on tweaking will sharpen your feel for how cointegration shows up in real price data.