A lot of new traders think Tesla and gasoline prices move opposite to each other, so they try to hedge TSLA with oil or gasoline ETFs.

It sounds simple, but real market data shows the link is much messier and doesn’t always hold.

We can use Python and statistics to test the relationship.

Students in Getting Started With Python for Quant Finance learn to measure rolling correlations, test co-movement with real data, and use statistical backtesting to see when a trade idea—like a TSLA-UGA hedge—actually works.

Here’s a snapshot of how it works, while the complete method is taught step by step in course.

By reading today’s newsletter, you’ll get Python code to analyze TSLA and UGA relationship and visualize their rolling correlation.

Let's go!

Trade the arb between TSLA and gasoline

Tesla–UGA correlation measures how Tesla stock moves relative to US gasoline prices, captured by the UGA ETF. This relationship is often touted as inverse, but in reality, it’s unstable and context-dependent.

That brings us to how this view emerged.

Tesla’s growth fueled interest in how EV adoption might respond to energy prices, with researchers and brokerages like Morgan Stanley and Bernstein publishing correlation studies during major oil shocks in 2008 and 2022. Some academic work shows brief, moderately negative correlation when gas prices spike, but long-term patterns break down due to broader market and policy effects. Real-world adoption data repeatedly proves the relationship is not as strong or lasting as headlines suggest.

So, how do professionals actually use this correlation?

Traders sometimes use TSLA–UGA moves to signal sentiment, especially after oil price shocks. Portfolio managers treat this relationship as a short-term indicator and always cross-check signals with actual sales, policy, and macro trends.

Let’s see how it works with Python.

Imports and setup

We use itertools to help with chart colors, matplotlib for plotting, scipy for statistics, yfinance to pull prices, and pykalman for smoothing price series with a Kalman filter.

1from itertools import cycle
2import matplotlib.pyplot as plt
3import scipy
4import yfinance as yf
5from pykalman import KalmanFilter
6
7color_cycle = cycle(plt.rcParams["axes.prop_cycle"].by_key()["color"])

Here, we download daily closing prices for TSLA and UGA since January 2020 using the yFinance library, then remove any missing values. Then we initialize a Kalman filter. The filter helps us smooth out noise in financial time series so we can see longer-term trends more easily.

1start_date = "2020-01-01"
2prices = yf.download(["TSLA", "UGA"], start=start_date).Close.dropna()
3
4kf = KalmanFilter(
5    transition_matrices=[1],
6    observation_matrices=[1],
7    initial_state_mean=0,
8    initial_state_covariance=1,
9    observation_covariance=1,
10    transition_covariance=0.01,
11)

The code above brings in all our tools, prepares them for analysis, and loads up our dataset. The Kalman filter settings allow us to apply a gentle smoothing process to raw price movements for TSLA and UGA. By getting this foundation in place, we can directly analyze and visualize how price trends evolve over time using both raw and smoothed data.

Visualize smoothed and raw price series

Here we use the Kalman filter to smooth both TSLA and UGA price series, then plot both moving averages together on the same chart using Matplotlib’s dual y-axis.

1scores_uga, _ = kf.filter(prices.UGA)
2scores_tsla, _ = kf.filter(prices.TSLA)
3
4_, ax1 = plt.subplots()
5ax1.plot(prices.index, scores_tsla, color=next(color_cycle), label="TSLA MA")
6plt.xlabel("Date")
7plt.ylabel("TSLA Price MA")
8ax2 = ax1.twinx()
9ax2.plot(prices.index, scores_uga, color=next(color_cycle), label="UGA Price MA")
10plt.ylabel("UGA Price MA")
11plt.show()

In these plots, we see how the Kalman filter helps us reduce day-to-day noise and spot broader movements. The moving average line provides a clean view of what direction prices are generally trending. Using dual axes makes it easy to compare two unrelated securities over time, even if their price levels are very different.

The result is a plot that looks like this.

Measure and visualize statistical relationships

This block defines a function that explores how price movements in the two assets are related over different time lags, using Spearman correlation from the scipy library.

It visualizes the correlation at various offsets to spot where the strongest similarities or lead-lag relationships occur.

1def find_offset(ts1, ts2, window):
2    l = len(ts1)
3    max_i_spearman = -1000
4    max_spearman = -1000
5    spear_offsets = []
6
7    for i in range(window, 0, -1):
8        series1 = ts1[i:]
9        series2 = ts2[: l - i]
10        spear = scipy.stats.spearmanr(series1, series2)[0]
11        spear_offsets.append(spear)
12
13        if spear > max_spearman:
14            max_spearman = spear
15            max_i_spearman = -i
16
17    for i in range(0, window):
18        series1 = ts1[: l - i]
19        series2 = ts2[i:]
20        spear = scipy.stats.spearmanr(series1, series2)[0]
21        spear_offsets.append(spear)
22        if spear > max_spearman:
23            max_spearman = spear
24            max_i_spearman = i
25
26    print("Max Spearman:", max_spearman, " At offset: ", max_i_spearman)
27    plt.plot(
28        range(-window, window), spear_offsets, c="green", label="Spearman Correlation"
29    )
30    plt.xlabel("Offset Size (Number of Business Days)")
31    plt.ylabel("Spearman Correlation")
32    plt.legend(loc=3)
33    plt.show()

By running the function below, we examine how smoothed price movements in TSLA and UGA are correlated at different lags and leads, and compare these results to the raw price series.

1print("Kalman-Filtered Smoothed Data")
2find_offset(scores_tsla, scores_uga, 200)
3print("Raw Data")
4find_offset(prices.TSLA, prices.UGA, 150)

The result is two plots.

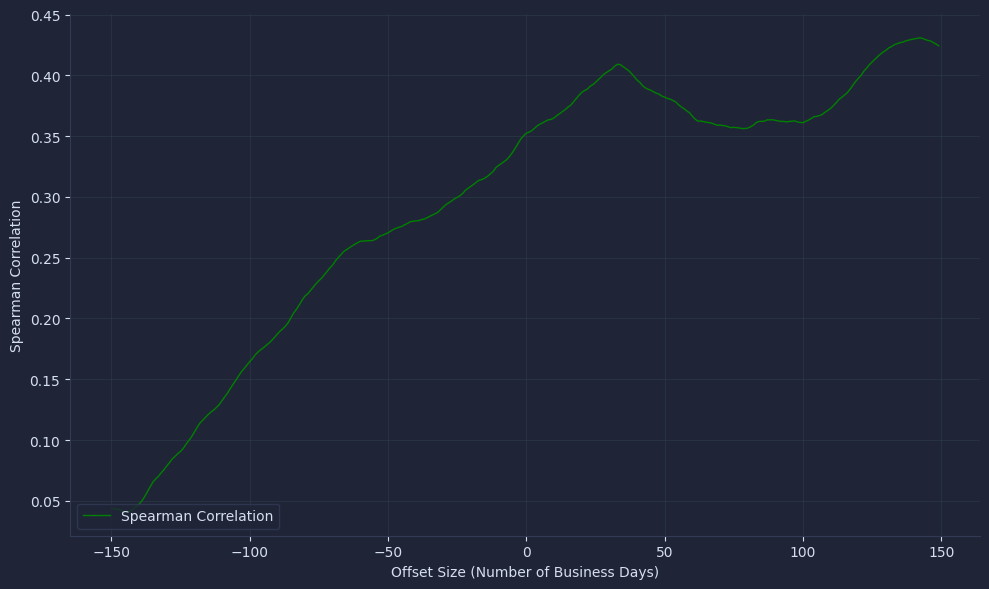
This function shows how the price actions of our selected tickers are statistically connected, even when separated by a number of business days.

By scanning across a range of offsets, we highlight where these relationships are most similar, which can point to leadership or lagging effects.

Visualizing the correlation results helps us see hidden trends or dependencies between assets beyond what raw plots may show.

Compare offset moving averages directly

This block lines up the smoothed price series for TSLA and UGA with a specific time offset (here, 140 business days apart) and displays both moving averages on the same chart for easy visual comparison.

1d = 140
2
3cseries1 = scores_tsla[d:]
4cseries2 = scores_uga[: len(scores_tsla) - d]
5r = range(len(cseries1))
6
7_, ax1 = plt.subplots()
8ax1.plot(r, cseries1, color=next(color_cycle), label="TSLA MA")
9plt.xlabel("Number of Business Days Elapsed")
10plt.ylabel("TSLA Price MA")
11plt.legend(loc=2)
12ax2 = ax1.twinx()
13ax2.plot(r, cseries2, color=next(color_cycle), label="UGA Price MA")
14plt.ylabel("UGA Price MA")
15plt.legend(loc=4)
16plt.title(f"{d} Day Offset")
17plt.show()

The plot looks like this.

Here we directly compare the trends of both moving averages, visually shifting one series by a significant number of days. This kind of alignment lets us see whether patterns from one asset appear later in the other. Using offset comparisons like this is a hands-on way to uncover possible leading or lagging relationships in how different asset prices move over time.

The chart shows that when UGA (gasoline prices) moves first, TSLA (Tesla stock) tends to follow roughly 140 business days later.

A trader could interpret this lagged correlation as a potential leading indicator, using major directional changes in UGA’s moving average as early trading signals for TSLA.

Your next steps

You can now spot trends and lagged correlations between TSLA and UGA with efficient Kalman smoothing and correlation tools.

Try changing the tickers in the yf.download line to explore different assets. Adjust the KalmanFilter parameters for more or less smoothing and rerun the analysis.

Play with the offset parameter in the final block to see how shifting time windows changes the dynamics you uncover.