I’ve been reviewing some risk frameworks this week.

(It’s always a good reminder that edge is only real if can keep your profits!)

Many beginners skip risk sizing, or follow a “2% rule” without ever checking if it actually fits their strategy.

Students in ​Getting Started With Python for Quant Finance​ learn how to collect live win rate and return data, test position sizing formulas in Jupyter notebooks, and run statistically honest backtests using VectorBT.

They see how parameters like risk, reward, and edge work in practice, not just on paper.

Today’s newsletter walks through a piece of the end-to-end process my students master in full.

By reading today’s newsletter, you’ll get Python code to calculate and apply the Kelly Criterion for your own trading risk management.

There's some hardcore quant code today, but don't worry. Just copy and paste it in Jupyter to get it working. Then paste it into ChatGPT and ask it to explain it. Magic!

Let's go!

Using leverage? Optimize with Kelly

The Kelly Criterion is a position sizing formula that helps traders optimize long-term capital growth based on their statistical edge in trading.

It's about using actual win rates and risk-reward ratios to decide exactly how much of your account to risk per trade.

John L. Kelly Jr., an information theorist at Bell Labs, developed the Kelly Criterion in the 1950s. It was first used to solve problems in signal processing, then famously adapted by gamblers like Ed Thorp in blackjack and later by quantitative traders on Wall Street.

Professionals today use this framework to protect capital and avoid catastrophic drawdowns.

Traders estimate their edge with live data, then use fractional Kelly to size trades and weather market shocks. Fractional Kelly is preferred because it lowers drawdown risk and deals with uncertainty in edge estimation.

Let's see how it works with Python.

Imports and setup

This block loads all required Python libraries, configures reproducibility, and sets problem size for the simulation. It also turns off cvxopt's progress output.

1import math
2import cvxopt as opt
3import matplotlib.pyplot as plt
4import numpy as np
5from cvxopt import blas, solvers
6
7np.random.seed(89)
8solvers.options["show_progress"] = False
9n = 4
10nobs = 1000

We've imported several key libraries to handle everything from mathematical functions to advanced portfolio optimization. Setting the random seed makes our results repeatable every time we run the script.

Disabling the progress output from cvxopt keeps our notebook clean. The variables define the number of assets and number of simulated returns we'll use in the optimization later.

Define helper functions and simulations

This block defines helper functions to generate random portfolio weights, simulate returns, and build random portfolios. It also includes a function that finds risk and return for Kelly-optimal portfolios at different leverage levels.

1def rand_weights(n):
2    k = np.random.randn(n)
3    return k / sum(k)
4
5
6def gen_returns(asset_count, nobs, drift=0.0):
7    return np.random.randn(asset_count, nobs) + drift
8
9
10def random_portfolio(returns, weight_func):
11    w = weight_func(returns.shape[0])
12    mu = np.dot(np.mean(returns, axis=1), w)
13    sigma = math.sqrt(np.dot(w, np.dot(np.cov(returns), w)))
14    if sigma > 2:
15        return random_portfolio(returns, weight_func)
16    return sigma, mu
17
18
19def get_kelly_portfolios():
20    ww = np.dot(np.linalg.inv(opt.matrix(S)), opt.matrix(pbar))
21    rks = []
22    res = []
23    for i in np.arange(0.05, 20, 0.0001):
24        w = ww / i
25        rks.append(blas.dot(pbar, opt.matrix(w)))
26        res.append(np.sqrt(blas.dot(opt.matrix(w), S * opt.matrix(w))))
27    return res, rks

Here, we set up functions to help with all the main tasks in our simulation: creating random weights, simulating returns, and using those returns to evaluate random portfolios.

One function also iterates through different leverage values to trace out the Kelly-optimal portfolios' risk and return profile.

Keeping these actions modular lets us easily try different portfolio constructions and risk calculations later.

Simulate returns and optimize portfolios

This block generates simulated returns for all assets, constructs random portfolios, and solves for the efficient frontier using quadratic programming with cvxopt.

1return_vec = gen_returns(n, nobs, drift=0.01)
2stds, means = np.column_stack(
3    [random_portfolio(return_vec, rand_weights) for _ in range(500)]
4)
5
6k = np.array(return_vec)
7S = opt.matrix(np.cov(k))
8pbar = opt.matrix(np.mean(k, axis=1))
9
10G = -opt.matrix(np.eye(n))
11h = opt.matrix(0.0, (n, 1))
12A = opt.matrix(1.0, (1, n))
13b = opt.matrix(1.0)
14
15N = 100
16mus = [10 ** (5.0 * t / N - 1.0) for t in range(N)]
17
18portfolios = [solvers.qp(mu * S, -pbar, G, h, A, b)["x"] for mu in mus]
19
20returns = [blas.dot(pbar, x) for x in portfolios]
21risks = [np.sqrt(blas.dot(x, S * x)) for x in portfolios]
22
23res, rks = get_kelly_portfolios()

We create 1,000 simulated daily returns for each asset with a slight positive drift to reflect expected growth.

We run hundreds of random portfolios to see the spread of risk and return, then prepare the data for quadratic programming using cvxopt matrices.

We solve for the efficient frontier by varying a risk-aversion parameter and store all the optimal combinations of portfolio risk and return for plotting.

We also calculate the Kelly-optimal portfolios to compare how aggressive leverage changes expected return and risk.

Visualize portfolio results and Kelly curve

This block plots random portfolios, the efficient frontier, and Kelly portfolios to compare how each approach balances risk and expected return.

1f, ax = plt.subplots()
2plt.plot(stds, means, "o", markersize=2)
3ax.set_xlabel("Volitility")
4ax.set_ylabel("Return")
5plt.title("Optimal Portfolio with Kelly")
6plt.plot(risks, returns, "y-o", markersize=2)
7plt.plot(res, rks, color="lightgray", marker="o", markersize=1)
8plt.plot(res, np.array(rks) * -1, color="lightgray", marker="o", markersize=1);

We present a chart with three key data sets: random portfolios (blue dots), the efficient frontier (yellow line and dots), and different leverage points for Kelly-optimal portfolios (light gray).

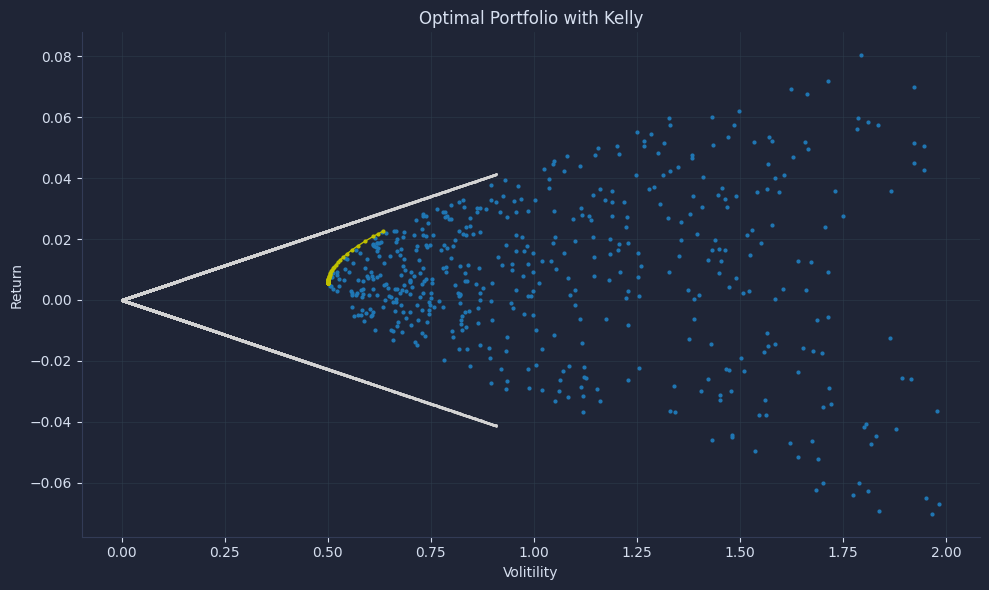
This lets us see, at a glance, how different portfolio choices trade off between risk and return.

The yellow curve represents the Kelly-optimal portfolios, showing where expected return grows fastest relative to volatility.

Each point on that curve maximizes geometric growth given the trader’s statistical edge and risk constraints.

In this context, those yellow dots are “optimal” because they balance leverage and risk precisely at the point where long-term capital growth is maximized without exceeding sustainable drawdown limits.

Your next steps

You’ve just built simulations comparing random, efficient frontier, and Kelly-optimal portfolios head-to-head. Try altering the drift in gen_returns to see how expected asset growth impacts portfolio shapes. Swap in your own asset return data for even more real-world insight. If you want to push further, adjust the constraints (G, h, A, b) to model shorting or allocation limits.